The name of my blog makes reference to adjunctions, so it seems appropriate that I at least say something about them. Really, there is a lot that can be said about these things, so I’ll stay (somewhat) focused on leading to a post I enjoyed from the n-Category Café (probably because I have an embarrassing grasp of sheaves). Before that, though, what even is an adjunction?
This might seem inaccessible, but there are numerous examples to help get accustomed to adjoints:
- Probably the simplest example of an adjunction is currying from computer science. Suppose you have a function (of sets)
. Explicitly, this assigns some element
for every
and
. This means that if we “partially evaluate” the function
just at some point
, we should get a function
. In other words, we can think of a function
equivalently as a function
that maps elements of
to functions
. This is an adjunction
.
- A common family of examples come from free-forgetful adjunctions. This point of view is mostly conceptual, since “forgetful functors” don’t usually have any precise definition. The idea is that we have a functor
which “forgets” something about objects of
that make them land in
. Then, if it exists, a left adjoint
tries to give that forgotten structure back in the easiest way possible.
- For example, consider the functor
which forgets the vector space structure on a set. This functor has a left adjoint
which sends a set
to the vector space whose basis is given by the elements of
. The adjunction just reflects the fact that in order to define a linear transformation
from a vector space with basis
into any other space
, it is enough to specify where
sends the basis vectors
—that is, a function
from the basis to the underlying set of
.
- Similarly, consider the functor
that forgets the group structure on a set. This also has a left adjoint
which sends a set
to the free group
generated by the elements of
. Again, the adjunction just says that a group homomorphism
is completely determined by where it sends the generators (elements of
).
- As a final algebraic example, consider the functor
that forgets the ring structure on a set. The left adjoint
sends a set
to the ring
of integer coefficient polynomials whose variables are the elements of
. The adjunction says that a ring homomorphism
is determined by where these variables get sent.
- Here’s a non-algebraic example. Consider the functor
that forgets the topology on a set. The left adjoint
realises a set as a discrete space. The adjunction says that any function out of a discrete space is automatically continuous.
- The forgetful functor in this case also has a right adjoint (which I guess you could call cofree)
which realises a set as a codirscrete space. The adjunction here says that any function into a codiscrete space is automatically continuous.
- The forgetful functor in this case also has a right adjoint (which I guess you could call cofree)
- For example, consider the functor
- Fix categories
and
. Consider the diagonal functor
which sends an object of
to the constant functor
on that object. Then,
has a right adjoint if and only if
has all limits of shape
. Dually,
has a left adjoint if and only if
has all colimits of shape
. Therefore, in a complete and cocomplete category
, we get an adjoint triple
for any (small) category
.
Side note: Compare all of the examples of free-forgetful adjunctions to the corepresenting objects of the forgetful functors mentioned in my previous post (so that elements of an object
just correspond to morphisms
). What are the free objects on the singleton set in each case? Any forgetful functor
with a left adjoint
is in fact corepresented by
, in the sense that the elements of the underlying set to an object
are precisely the morphisms
. This boils down to the fact that elements of a set
are just morphisms
.
Fix an adjoint pair . For any
, we have an identity morphism
in
, and its corresponding morphism
is called the adjunction unit at
. Dually, the identity morphism
for any
induces an adjunction counit
.
| Adjunction | Unit | Counit |
|---|---|---|
| Currying |
The evaluation map |
"Coevaluation" |
| Free-forgetful |
The "inclusion" |
The "projection" |
| Limit |
The isomorphism |
The universal cone |
From the examples, you can see that sometimes the adjunction unit or counit may have a useful meaning by itself, but the real benefit is that they give us general formulae for and
. Explicitly, the right adjunct of a morphism
is given by
, and the left adjunct of a morphism
is given by
.
In particular, this allows us to use the adjunction unit and counit to understand how adjoint functors act on morphisms (and vice versa):
Proposition 2: Given an adjoint pair , we have that
is faithful (resp. full) if and only if the adjunction unit
is monic (resp. split epic)—that is, if and only if the adjunction unit is injective (resp. surjective) on generalised elements—for every object
. Dually,
is faithful (resp. full) if and only if the adjunction counit is epic (resp. split monic) on every object.
Proof. Suppose in
, then we can compute
with
. Indeed, this follows from the computation
, recalling that
. Therefore,
if and only if
(using that
is bijective). In particular, this means that
is faithful if and only if
is monic. On the other hand,
if and only if
. Since every generalised element
is of the form
for some
(namely
), this means that
is full if and only if
is surjective on generalised elements.
Corollary 3: Given an adjoint pair , the following are equivalent:
and
are both fully faithful.
is an (adjoint) equivalence of categories.
is an (adjoint) equivalence of categories.
Given a functor with right adjoint
, consider the full subcategory
of those objects
for which
is an isomorphism. Note that this subcategory is replete (i.e., closed under isomorphisms): if
and
, then naturality of the adjunction units gives a diagram

where three out of four maps are isomorphisms. This forces to be an isomorphism also, and the claim follows. In particular, this implies by definition that anything in the essential image of
maps back into
via
. If we denote the essential image by
, then this means that our adjoint pair restricts to an adjoint pair
where
is an equivalence (it is essentially surjective by definition, and fully faithful by Proposition 2). By Corollary 3, this gives us the following fact:
Lemma 4: An adjoint pair restricts to an adjoint equivalence
, where
is the full subcategory in
of objects for which the adjunction unit is an isomorphism, and
is likewise the full subcategory in
of objects for which the adjunction counit is an isomorphism. Moreover, these subcategories are maximal with this property.
Farming for Equivalences
Lemma 4 is an interesting one, because from what I’ve given as examples of adjunctions, it doesn’t seem to say a whole lot:
- Consider the currying adjunction
. For coevaluation
to be bijective, this would mean all functions
have to be of the form “
” for some
. This is only possible if either
is empty (so that there is at most one map
) or
(so that the map takes at most one value, and the
coordinate is uniquely determined).
- To summarise: if
is a singleton set, then currying reduces to just being the identity functor on
; otherwise, then Lemma 4 gives us an equivalence between terminal categories (categories with one object and one morphism). In either case, the equivalence is trivial.
- To summarise: if
- The free-forgetful adjunctions listed above are not that exciting either. Since the free vector space (similarly group, commutative ring) on a set
is always strictly larger than
(in the sense that the inclusion is never surjective), the free-forgetful adjunction on spaces induces an equivalence of empty categories.
- For topological spaces, the equivalence is mildly notable. For the adjunction
, the adjunction unit is the identity map, and Lemma 4 produces the equivalence between sets and discrete topological spaces. Likewise, for the adjunction
, the adjunction counit is the identity map, and Lemma 4 produces an equivalence between sets and codiscrete topological spaces (… though this identification is seldom useful, from what I’ve seen).
- Equally remarkable as the above example, consider limit adjunction
. The adjunction unit is again always an isomorphism, and so Lemma 4 gives the equivalence between a category
and the full subcategory of
on (essentially) constant diagrams. Incredible. You get the same equivalence when looking at the colimit adjunction.
Perhaps the equivalence in Lemma 4 reflects how destructive an adjunction is on the objects? For instance, the action of forgetting the underlying vector space structure is irreparable: you can never recover a reasonable vector space structure once you lose it (and likewise, taking a set as a basis for a space makes it impossible to recover the set since there are countless possible bases to choose from for any given vector space). On the other hand, forgetting the topology of a space is only destructive if the topology were nondiscrete (or dually, nontrivial), and it’s easy to recover a set once it’s endowed with a topology. Similarly, limits reduce an entire diagram to a single object, which is destructive unless the diagram were essentially constant.
With all of these trivial applications of Lemma 4, it comes as even more of a surprise (at least to me) that you might actually get something in some cases. Some examples can be found in and around this answer to a MathOverflow post. The example I’m more interested in right now is—you guessed it—the one to do with sheaves. What are sheaves? The beautiful thing is that we’ll find out through Lemma 4 (if you’re willing to join me through some elaborate abstract computations).
Let’s start with this wonderful abstract nonsense construction. Suppose we have some category (of “shapes”) and some functor
(which we can think of as realising these abstract shapes concretely as objects of
). This functor induces a backwards-pointing functor
into the category of presheaves of
defined on
as
. If
is cocomplete, then
admits a left adjoint
which sends a presheaf
to the coend
This is the nerve-realisation adjunction, where the right adjoint is called the nerve, and the left adjoint
the realisation. For example, if you take
to be the simplex category and
, you recover the geometric realisation of simplicial sets, which is left adjoint to the singular simplicial complex of topological spaces.
Side note: In the case of geometric realisation, Lemma 4 again does not give anything useful: the singular complex of the geometric realisation of any non-discrete simplicial set is going to be much bigger than the original simplicial set, even just on the level of 0-cells. Therefore, Lemma 4 gives us an equivalence between discrete simplicial sets (constant functors , aka sets) and discrete topological spaces. However, this adjunction defines a Quillen equivalence between model categories, which tells us that this adjunction translates the homotopy theory of each category perfectly well (or even fancier, this adjunction induces an equivalence of their corresponding
-categories).
Let’s look at the special case that is supposed to explain what sheaves are. This should (hopefully) clarify some of the abstract nonsense of the general construction.
The setup is as follows. Fix a topological space , then we want
to be the poset of open subsets of
. On the other hand, take
to be the slice category of topological spaces equipped with a continuous map
. The functor
is the canonical one that sends an open subset
to the inclusion of spaces
. Now we have our desired adjunction
The nerve functor is easiest to understand, so let’s look at it first. Given a space , the nerve
is the presheaf that sends an open set
to the set of those maps
that lie over
in the sense that

commutes. This means that is the set of local sections of
over
defined on
. Therefore, given a presheaf
, we should think of
as the set of local sections of some abstract topological space (which we hope to be
) defined over
. Under this perspective, an inclusion
of open subsets induces a map
which we think of as restricting a section over
to the subset
.
So how do we construct the corresponding space ? We need each
to be a local section of some kind, so start by taking a copy
of the open
for every
, with the inclusion
. This ensures that there is a canonical choice for a local section of
for each
—namely, the map
. The challenge is to now make sure that these are the only sections, so we have to start gluing these individual spaces together in an appropriate way for all opens
.
For an inclusion , we need to make our interpretation of
as “restricting local sections” literal. For a local section
, write
for its “restriction” to
, then we have to realise
as a subset of
. We formalise this identification by taking the pushout of the inclusion
along the map
that sends
. In fact, performing this pushout simultaneously over all inclusions
is precisely what it means to take the coend
.
As one might expect (from all of my buildup about talking about sheaves), this construction of fails to realise
as the presheaf of local sections for a space in general. For any open set
, there is a canonical mapping
which sends
to the canonical local section
, but this is not a bijection in general. In fact, it may not even be injective.
- For genuine local sections
, suppose that
is a cover of open sets such that
for every
. As these are genuine functions, this necessarily implies
. Therefore, for the map
to be injective, we need the same to be true for
when restricted to open covers.
- Likewise, for genuine functions, it is clear that if
is a cover of opens, and we have functions
that are compatible in the sense that
for all
, then we have a well-defined function
such that
. Thererfore, for the map
to be surjective, we need to ensure the same is true when given compatible sections
for
.
These turn out to be sufficient for to be a natural isomorphism, and any presheaf
satisfying the above conditions is then called a sheaf. Therefore, on the left hand side, we find that Lemma 4 gives us the category
of sheaves on
. In fact, notice how
is always a sheaf (aptly called the sheaf of local sections of
over
). Therefore, the adjunction unit actually defines the sheafification
of any presheaf
, which is left adjoint to the canonical inclusion of sheaves as presheaves.
What about in the other direction? When is a space homeomorphic to
? We have a canonical map
which is induced by sending each
to
through the given local section
. Suppose this map is a homeomorphism. For any point
, we can find a sufficiently small neighbourhood
such that this map
restricts to
. If this map is a homeomorphism, then so is
, and so we have a local inverse
. Since everything lies over
, this forces
to be the restriction of the map
to
. Since homeomorphisms are bijective, this implies that
is a local homeomorphism. In French, such a space is called an espace étalé (meaning “spread-out space”), and we can see that any espace étalé is homeomorphic to the nerve of its sheaf of local sections. Therefore, we find an actually nontrivial incarnation of Lemma 4:
Summary: The canonical inclusion for any topological space
induces—by the nerve-realisation adjunction and Lemma 4—an equivalence of categories
between the category of sheaves on
and the category of espaces étalés over
.
In principle a similar argument should work for all nerve-realisation adjunctions. However, things might get hairy if your shape category is not a poset. Even then, we used a lot of facts about topology to get a nice characterisation of both
and
… How then do we generalise this construction?
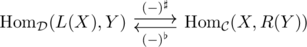
9 thoughts on “An adjunct to adjunctions”