Maintain certain limits for an enriched experience

The idea behind enrichment is that sometimes your category is more than just a “fancy set theory” —sometimes it’s fancy linear algebra, or fancy topology… or even fancy category theory. Prototypical examples usually come from observing that morphisms in your category carry some additional canonical structure: not only can you compose linear transformations, but you can add them together (pointwise), which makes all hom-sets into abelian groups. This reflects that vector spaces are “abelian groups with extra structure.”

Note. Of course, the hom-sets between vector spaces are even vector spaces, which just says that vector spaces are vector spaces with (no) extra structure…

A lot of the time, enrichment is canonical, in the sense that it just feels like the obvious choice for the enrichment: pointwise addition of morphisms is still a morphism, so this defines a canonical enrichment in abelian groups for vector spaces. However, there are some cases where the enrichment is more than canonical: it’s forced by the properties of the category!

The point I’m trying to make

The simplest example is enrichment in pointed sets. Let $(\mathbf{Set}_*,\wedge,\{0,1\})$ be the symmetric monoidal category of pointed sets (under smash product). Enrichment over this category is the same as having a zero morphism between any pair of objects (which annihilate all other morphisms under composition). We have the following result:

Proposition 1. Let $\mathcal C$ be a category with an initial object $\emptyset$ . Then, the category is enriched over $\mathbf{Set}_*$ if and only if $\emptyset$ is also a terminal object (i.e., it’s a zero object). In either case, the enrichment is unique.

Proof. If such a $\mathcal C$ is enriched over pointed sets, then we have a zero morphism $X\to\emptyset$ for any object $X$ , so that the initial object is already weakly terminal. To see that it is actually terminal, note that $\emptyset$ has a unique endomorphism, which must therefore be its zero morphism and identity morphism. Therefore, any morphism $f:X\to\emptyset\xrightarrow{\mathrm{id}}\emptyset$ must already be the zero morphism, making $\emptyset$ terminal.

Conversely, suppose we have a zero object $0$ . In particular, its unique endomorphism is simultaneously a zero morphism and an identity morphism as before. For any pair of objects $X,Y$ , we always have a unique map factoring through $0$ given by $X\xrightarrow!0\xrightarrow{\mathrm{id}_0}0\xrightarrow!Y$ , and this must be a zero morphism since $\mathrm{id}_0$ is. Since zero morphisms are unique, this makes the $\mathbf{Set}_*$ -enrichment necessarily unique. $\blacksquare$

To add it all up

The prototypical example I had in mind is enrichment over the symmetric monoidal category $(\mathbf{CMon},\otimes_{\mathbb{N}},\mathbb{N})$ of commutative monoids (where the tensor product ensures that $(m+m')\otimes n = m\otimes n + m'\otimes n$ and similarly for the other argument). In this setting, we get a very similar result.

Proposition 2. Let $\mathcal C$ be a category with finite coproducts. Then, the category is enriched over $\mathbf{CMon}$ if and only if its finite coproducts also serve as products in a compatible way; that is, they form biproducts. In either case, the enrichment is then unique.

Proof. If $\mathcal C$ is enriched over commutative monoids, then for objects $X,Y$ , we need to show that $X\sqcup Y$ satisfies the universal property of a product (we have already seen this for the initial object). Indeed, we have a projection map $\pi_X:X\sqcup Y\to X$ given by cotupling $\mathrm{id}_X$ and $0:Y\to X$ , and similarly for $\pi_Y:X\sqcup Y\to Y$ . If we have maps $f:Z\to X$ and $g:Z\to Y$ , then we have a map $Z\to X\sqcup Y$ given by the sum $\iota_Xf + \iota_Yg$ . This is moreover uniquely compatible with the projection maps defined above because $\iota_X\pi_X+\iota_Y\pi_Y = \mathrm{id}_{X\sqcup Y}$ (and thus we need only look at the projected components of any other candidate $Z\to X\sqcup Y$ ). Note that by being defined this way, the coproduct becomes a biproduct.

Conversely, suppose we have biproducts. We have already seen that the zero morphisms are completely determined by the consequent zero object, so we need only construct a sum that is compatible with composition. Let $X,Y$ be objects, then the sum of morphisms $f,g:X\to Y$ is given by $X\xrightarrow{\Delta_X}X\oplus X\xrightarrow{f\oplus g}Y\oplus Y\xrightarrow{\nabla_Y}Y$ . Equivalently, this summation rule is given by either path in the commutative diagram

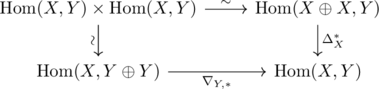
(which makes compatibility with composition more self-evident). Uniqueness follows from the fact that, given $\mathbf{CMon}$ -enrichment, retracing the above construction with the biproducts defined in the first paragraph recovers the original enrichment. Note that this crucially uses the biproduct structure of these co/limits (both in ensuring the above enrichment makes sense, and in ensuring it does not depend on the choice of biproducts). $\blacksquare$

If we do not start with a biproduct structure, then the above enrichment will not make sense. Indeed, just consider the usual direct sum of abelian groups, but negate every projection map. The above construction would then give the “addition” rule $f\mathbin{\widehat+}g = -(f+g)$ , which is not associative since $f \mathbin{\widehat+}(g \mathbin{\widehat+} h) = f \mathbin{\widehat+} (-g-h) = -f + g + h$ whereas $(f \mathbin{\widehat+} g) \mathbin{\widehat+} h = -(f-g) \mathbin{\widehat+} h = f+g-h$ . (It doesn’t respect the neutral element either.)

Remark. Not that it’s particularly useful, but this argument can be modified to apply to $\kappa$ -ary commutative monoids for any regular cardinal $\kappa$ , which has both of the above proofs as special cases. (Technically, any ordinal is fine, but induction and associativity would allow us to pump the arity up to the next regular cardinal.) Then, we have canonical enrichment over $\mathbf{CMon}_{\kappa\text{-ary}}$ iff we have $\kappa$ -small coproducts which are biproducts.

Why commutative?

I mean, it’s clear that co/products are about as symmetric as it gets, so there’s your answer.

But even just a bit more generally: why does enrichment only seem to work with commutative monoids, or abelian groups? If you take the usual definition of enrichment, this just boils down to the fact that pointed sets, commutative monoids, abelian groups, etc. all have a meaningful tensor product.

Interestingly, I never really mentioned these tensor products when talking about these unique enrichments. This is partially due to laziness on my part: shadows of these tensor products appear when I mention that zero morphisms annihilate anything else under composition, or when I use that composition is additive in each component. The natural question that came to my mind regarding the tensor product was this: if the enrichment of these (sufficiently cocomplete) categories is so canonical, is the tensor product canonical as well?

Unlike the immediate (I only care about locally small categories if enrichment is on my mind) $\mathbf{Set}$ -enrichment of all categories, none of the tensor products for pointed sets, commutative monoids, abelian groups, and so on, are given by the categorical product. However, they’re still less arbitrary than a general (symmetric) monoidal structure, because they’re still defined by a universal property. I’ll get to this in a bit.

You don’t really need a tensor product to talk about enrichment. The primary raison d’être for tensor products in this context is to allow you to put hom-objects “side-by-side” for the sake of defining composition and the like. There are workarounds in the situation where a tensor product isn’t present, but tensor products make life the easiest. However, if you just wanted to put objects side-by-side for the sake of having out-going maps, but don’t want the headache of trying to work with tensor products, then you can just work with multicategories.

Honestly, I’m not very fond of weird generalisations of categories like these (they seem too niche, even for me), but they keep popping up (even in my master’s thesis), so here we are. A multicategory is just a category where morphisms—now cleverly called multimorphisms—are allowed to have arbitrary (finite) arity. (In particular, every multicategory has an underlying ordinary category by restricting attention to just the unary morphisms.) Now, you can define enrichment in a multicategory in essentially the same way as enrichment in a monoidal category: now, identity morphisms are given by nullary morphisms $()\to\mathrm{Hom}(X,X)$ , and composition is given by binary morphisms $(\mathrm{Hom}(Y,Z),\mathrm{Hom}(X,Y))\to\mathrm{Hom}(X,Z)$ .

The reason why I’m bringing multicategories up is because they can help make sense of categories whose hom-sets might have any sort of structure. To be more precise: given a concrete category $\mathcal C$ (so that it has a faithful forgetful functor $U:\mathcal C\to\mathbf{Set}$ , but no other assumptions are necessary), you can define a multicategory $\mathcal C^{\mathrm{multi}}$ (this is an extemporaneous thing that I’m sure already exists in the literature, but I couldn’t find it) whose multimorphisms $(X_1,\dots,X_p)\to Y$ are given by those (set-theoretic) functions $f:U(X_1)\times\dots\times U(X_p)\to U(Y)$ that are pointwise given by morphisms of $\mathcal C$ , meaning that for all $x_i\in X_i$ excluding some $j$ , the function $f(x_1,\dots,-,\dots,x_p) : U(X_j)\to U(Y)$ lies under some morphism $X_j\to Y$ in $\mathcal C$ .

This is the actual generalisation of multilinear maps and the like, which are what you get when you start with $\mathcal C = \mathbf{Vect}_{\Bbbk}$ or something. Now, this notion makes sense for categories where a tensor product doesn’t really exist, such as in the category of all monoids, or the category of groups. I should mention that this is a “conservative” extension: a monoidal category can be equivalently defined as a multicategory whose hom-functors $\mathrm{Hom}(X_1,\dots,X_p;-)$ (when restricted to the underlying ordinary category) are all corepresentable, with the corepresenting objects given by the $p$ -fold tensor products $X_1\otimes\dots\otimes X_p$ . If you actually take the concrete category to be the category of pointed sets, commutative monoids, abelian groups, etc., the induced multicategory is exactly the same as the multicategory corresponding to their canonical tensor products—this is the usual universal properties of these tensor products!

Technical note. Corepresentability of the multi-homs is necessary, but insufficient. You need to assert that the induced morphisms such as $X\otimes Y\otimes Z\to X\otimes(Y\otimes Z)$ are all isomorphisms as well.

Now that I’ve shown that it is in principle possible to enrich over arbitrary groups or monoids, let me negate it all by mentioning that enriching in these (multi)categories is really hard. If a category is enriched in noncommutative monoids, then this means all hom-sets have some sort of multiplication such that composition preserves the multiplication in each variable separately. This means that if $f,g$ are parallel and both composable with $h$ , then $h\circ(f\cdot g) = (h\circ f)\cdot(h\circ g)$ . The problem arises if $h'$ is parallel to $h$ . Now, we would need that

$(h\cdot h')\circ(f\cdot g) = ((h\cdot h')\circ f)\cdot((h\cdot h')\circ g) = (h\circ f)\cdot(h'\circ f)\cdot(h\circ g)\cdot(h'\circ g)$

works out to the same morphism as

$(h\cdot h')\circ(f\cdot g) = (h\circ(f\cdot g))\cdot(h'\circ(f\cdot g)) = (h\circ f)\cdot(h\circ g)\cdot(h'\circ f)\cdot(h'\circ g)$

but this is very difficult to achieve unless the multiplication is commutative. If you were to take a one-object category enriched in nonabelian groups, you would find that the hom-group still turns out to be abelian and you recover a (noncommutative) ring^[cf], where the ring addition is given by the group structure, and the multiplication by composition. To get a one-object category with a noncommutative multiplication, you would need a noncancellative monoid. For example, let $M = \{1, a,b\}$ be the smallest noncommutative monoid, where $ab=a^2=a$ and $ba=b^2=b$ (it’s also noncancellative: strings of compositions are completely determined by the leading non-unit element). We can take this monoid structure to be both the composition rule and the enrichment monoidal structure due to the highly destructive nature of this monoidal structure.