Weekly local blog presents: weakly local presentability

If you’ve read the similar-sounding blog post already, then I don’t need to introduce this post. If you haven’t… then read it! (I’m joking, but I will be porting some stuff over from there.) In any case, I’m still mainly looking at [AR94].

Fix a regular cardinal $\kappa$ . Recall from Definition 1 in that old post that an object $X$ is $\kappa$ –small if $\mathrm{Hom}(X,-)$ preserves $\kappa$ -directed colimits. I didn’t make this definition explicit in the previous post, but here it is:

Definition 1. A (locally small) category is called $\kappa$ -accessible if:

it has all $\kappa$ -filtered colimits (or equivalently, all $\kappa$ -directed colimits)
it is generated by $\kappa$ -filtered colimits by $\kappa$ -small objects.

A functor $F:\mathcal C\to\mathcal D$ is called $\kappa$ -accessible if $\mathcal C, \mathcal D$ are $\kappa$ -accessible, and it preserves $\kappa$ -filtered (or directed) colimits.

From Definition 2 in my older post, we can see that a $\kappa$ -accessible category is locally $\kappa$ -presentable iff it is cocomplete. What’s maybe less clear is that a $\kappa$ -accessible category is also locally $\kappa$ -presentable iff it is complete [AR94, Corollary 2.47]. One implication is clear (because locally presentable categories are complete). For the converse, we get to dive a bit into some more adjunction stuff.

Let $\mathcal C$ be $\kappa$ -accessible and consider its full subcategory $\mathrm{Pres}_\kappa\mathcal C$ of $\kappa$ -presentable objects. This is still an essentially small category, just as for locally presentable categories, and is in fact dense in $\mathcal C$ . I just stated this fact in my old post, but let’s address it now, following [AR94, Proposition 2.8].

For any $X\in\mathcal C$ , write it as a filtered colimit $X=\varinjlim_iK_i$ of $\kappa$ -presentable objects. For any other $K\to X$ with $K$ also $\kappa$ -presentable, preservation of the above colimit means that the morphism factors through some $K_i\to X$ . This factorisation has to respect the shape of the colimit diagram, so if we have $\kappa$ -many such factorisations $K\to K_{i_\alpha}$ , then for any upper bound $K_{i_*}$ in the $\kappa$ -filtered diagram, we must have that $K\to K_{i_\alpha}\to K_{i_*}$ is independent of $\alpha$ . This shows two things: first, that $X = \varinjlim\left((\mathrm{Pres}_\kappa\mathcal C\downarrow X)\to\mathcal C\right)$ is a canonical colimit of presentables, and that this colimit is $\kappa$ -filtered.

Now we want to show that $\mathcal C$ is locally $\kappa$ -presentable once it is complete, and we already have a fully faithful embedding $\mathcal C\to\mathbf{PSh}(\mathrm{Pres}_\kappa\mathcal C)$ by density proven above. By the representation theorem, it then suffices to show that this embedding preserves $\kappa$ -filtered colimits and is reflective. Preservation of $\kappa$ -filtered colimits comes for free because the objects of $\mathrm{Pres}_\kappa\mathcal C$ by definition preserve such colimits, and colimits in a presheaf category are computed pointwise. (This means we have also shown that $\mathcal C$ is accessibly embedded into that presheaf category). Therefore, we need only find a left adjoint to this inclusion. However, we do not yet know that $\mathcal C$ is cocomplete, as we are only assuming it is complete.

In order to find a left adjoint, we appeal to an adjoint functor theorem.

General Adjoint Functor Theorem (Freyd). Suppose $R:\mathcal C\to\mathcal D$ is a continuous functor such that

the domain category $\mathcal C$ is locally small and complete
$R$ satisfies the solution set condition: for any $D\in\mathcal D$ , we can find a set $\{f_i:D\to R(X_i)\}_i$ that is weakly initial in $(D\downarrow R)$ , which is to say that any morphism $D\to R(X)$ factors through some $f_i$ .

Then $R$ admits a left adjoint.

Proof. Fix $D\in\mathcal D$ . Note that the weakly initial set $\{f_i:D\to R(X_i)\}$ induces a weakly initial object $f:D\to \prod_iR(X_i) = R\left(\prod_iX_i\right)$ because $R$ preserves limits. Let $X := \prod_iX_i$ and take $L(D)$ to be the equaliser of all endomorphisms of $X$ that define endomorphisms of $D\to R(X)$ . Then, $D\to R(L(D))$ is the initial object in $(D\downarrow R)$ . Therefore all maps $D\to R(Y)$ factor through the image under $R$ of some unique $L(D)\to Y$ . We can extend $L$ to a functor by taking $L(D)\to L(D')$ to be the unique morphism corresponding to $D\to D'\to R(L(D'))$ , and this defines our left adjoint $L\dashv R$ . $\blacksquare$

Now, it turns out given arbitrary $\kappa$ -accessible functors $\mathcal P\xrightarrow P\mathcal B\xleftarrow Q\mathcal Q$ that the comma category $(P\downarrow Q)$ is $\kappa$ -accessible [AR9, Theorem 2.43]. This implies the following:

Lemma 2. Acessible functors satisfy the solution set condition.

Proof. Let $F:\mathcal C\to\mathcal D$ be $\kappa$ -accessible, then we are just trying to show that $(D\downarrow F)$ has a weakly initial set for every $D\in\mathcal D$ . Since $F$ is $\kappa$ -accessible, so is this comma category, so every element is a canonical colimit of $\kappa$ -presentable objects. Therefore, $\mathrm{Pres}_\kappa(D\downarrow F)$ serves as a weakly initial family. $\blacksquare$

In particular, since $\mathcal C\to\mathbf{PSh}(\mathrm{Pres}_\kappa\mathcal C)$ is accessible, and it certainly preserves limits, it follows from the general adjoint functor theorem that it has a left adjoint, making $\mathcal C$ a reflective subcategory that is closed under $\kappa$ -filtered colimits; i.e., $\mathcal C$ is locally $\kappa$ -presentable.

I mentioned in the old blog post (somewhat in passing) that locally presentable categories can also be described as certain orthogonality classes of a presheaf category. More precisely, a full subcategory of a locally presentable category is locally $\kappa$ -presentable precisely if it is the orthogonality class of a set of morphisms between $\kappa$ -presentable objects, and this orthogonality class is closed under $\kappa$ -filtered colimits (or, equivalently, is closed under limits).

If we relax to the context of $\kappa$ -accessible categories, we can relax orthogonality to injectivity, and show that any (small-)injectivity class of an accessible category is an accessibly embedded subcategory [AR94, Proposition 4.7].

Definition 3. For a class $\mathcal M$ of morphisms in a category, an object $K$ is said to be $\mathcal M$ –injective if all morphisms $A\to K$ can factor through any morphism $(A\to A')\in\mathcal M$ via some extension (or I might say “lift”) as per the diagram

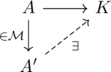
If the extension is unique for any $(A\to A')\in\mathcal M$ , then $K$ is called $\mathcal M$ –orthogonal. Denote by $\mathrm{Inj}(\mathcal M)$ the full subcategory of $\mathcal M$ -injective objects, and by $\mathcal M^\perp$ the full subcategory of $\mathcal M$ -orthogonal objects.

If $\mathcal M$ is the class of all monomorphisms, then $\mathrm{Inj}(\mathcal M)$ is just the collection of injective objects (in the original sense). Note that if the category has a terminal object, then $K$ being $\mathcal M$ -injective is equivalent to saying that $K\to*$ satisfies the right lifting property against $\mathcal M$ .

Since locally presentable categories are (among) the orthogonality classes of presheaf categories, we might expect from how all accessible categories embed accessibly into a presheaf category that we could extend this result to saying all accessible categories are (among) the injectivity classes of presheaf categories. While this isn’t quite the case, we can characterise injectivity classes of presheaf categories in a similar way [AR94, Theorem 4.8]:

Theorem 4. A full subcategory of a locally presentable category is a $\kappa$ -injectivity class (i.e., injective wrt morphisms with $\kappa$ -presentable domains and codomains) iff it is $\kappa$ -accessibly embedded and closed under products in $\mathcal K$ .

Sketch. We already mentioned one direction (closure under products is clear). Suppose $\mathcal C$ embeds $\kappa$ -accessibly into a locally presentable category $\mathcal K$ and is closed under products. For every $K\in\mathrm{Pres}_\kappa\mathcal K$ , choose a weakly initial family $\{f_i:K\to \iota(X_i)\}$ in $(K\downarrow\iota)$ , then we have a weakly initial $K\to X=\prod_iX_i$ because of closure under products. Choose any $r_K:K\to K'\in\mathrm{Pres}_\kappa\mathcal K$ that factors through this weakly initial morphism, then evidently any morphism $K\to X$ with $X\in\mathcal C$ factors through $r_K:K\to K'$ . By taking $\mathcal M := \{r_K \mid K\in\mathrm{Pres}_\kappa\mathcal K\}$ , it turns out that $\mathcal C=\mathrm{Inj}(\mathcal M)$ . $\blacksquare$

Since accessible categories are locally presentable once they’re complete, we see from the above that locally presentable categories are precisely the complete $\kappa$ -injectivity classes of a presheaf category (or any other locally presentable category, I suppose). For this reason, we may call general $\kappa$ -injectivity classes of a locally presentable category weakly locally $\kappa$ -presentable categories.

In fact, weakly locally presentable categories look a lot like locally presentable categories [AR94, Theorems 4.11 and 4.13]:

I want to say a bit more about the last row. First, recall that a sketch consists of a small category $\mathcal S$ , sets $L,C$ of diagrams, and an assignment of every diagram in $L$ a cone, and every diagram in $C$ a cocone. Accordingly, a model for $\mathcal S$ is a functor that sends every cone for $L$ to a limit cone, and every cocone for $C$ to a colimit cocone.

Categories of models of a sketch are always accessible, and in fact the converse is also true [AR94, Theorems 2.58 and 2.60]: for a $\kappa$ -accessible category $\mathcal C$ , take the following sketch:

choose a set $L$ of representative $\kappa$ -small diagrams of corepresentables in $\mathbf{coPSh}(\mathrm{Pres}_\kappa\mathcal C)$ , and assign to each diagram $D$ their limit $\varprojlim D$
then, take the sketch to be the full subcategory of $\mathbf{coPSh}(\mathrm{Pres}_\kappa\mathcal C)$ on the representables as well as $\varprojlim D$ for every $D\in L$
the set of sketched limit cones are as in $L$ , and the set of sketched colimit cocones are the canonical cocones to each $\varprojlim D$ for $D\in L$

Note that this sketch is normal in the sense that the sketched co/limit co/cones are already co/limits in the sketch category. This means all models of sketches can be improved to models of normal sketches.

If $C=\varnothing$ , then the sketch is called a limit sketch. We have already seen that all locally presentable categories are categories of models for a limit sketch.

Now, recall that a morphism $f:X\to Y$ is an epimorphism iff the square

is a pushout square (the universal property is exactly the definition of being epi). Accordingly, a limit-epi sketch is a limit sketch where we adjoin the above squares as sketched colimit diagrams. Equivalently, a limit-epi sketch specifies which cones should be realised as limits, and which morphisms should be epimorphisms.

To realise a weakly locally presentable category $\mathcal C$ as the category of models for a limit-epi sketch, take the sketch $\mathcal S$ obtained from the fact that weakly locally presentable categories are accessible, and then modify the sketched colimits as follows. Since $\mathcal C$ has weak colimits, $\mathcal C^{\mathrm{op}}$ has weak limits, and in fact for any diagram of $\kappa$ -presentable objects, we can find a $\kappa$ -presentable weak limit. Therefore, instead of taking the canonical colimits to every $\varprojlim D$ , assert instead that the induced map $\mathrm{wk}\varprojlim D\to\varprojlim D$ from a choice of $\kappa$ -presentable weak limit is an epi. The resulting categories of models end up being equivalent, so this realises $\mathcal C$ as the category of models for the above limit-epi sketch.

With all these parallels, it only really leaves one question: if locally presentable categories are models for essentially algebraic theories, then do weakly locally presentable categories correspond to something similar?

A locally $\kappa$ -presentable category is…	A weakly locally $\kappa$ -presentable category is…
A $\kappa$ -accessible category with colimits	A $\kappa$ -accessible category with weak colimits
A $\kappa$ -accessible category with limits	A $\kappa$ -accessible category with products
A $\kappa$ -accessibly embedded reflective subcategory of presheaves	A $\kappa$ -accessibly embedded weakly reflective subcategory of presheaves
A $\kappa$ -accessibly embedded $\kappa$ -orthogonality class of presheaves	A $\kappa$ -accessibly embedded (this is redundant) $\kappa$ -injectivity class of presheaves
The category of models for a $\kappa$ -small limit sketch	The category of models for a $\kappa$ -small limit-epi sketch

Share this:

Related

Leave a comment Cancel reply