How have I gone this long without talking about monads?

It really is something, especially since in the very homepage, I refer to this blog as the category of algebras for the “free thinking” monad… I have an ulterior motive for writing this post, so this isn’t going to be the best introduction to monads you’ve ever seen. If I find time, maybe I’ll give monads a proper post.

So anyway, what is a monad? There are many equivalent and terse ways of defining them floating around, for example:

Definition 1. A monad on a category $\mathcal C$ is a monoid in the category of endofunctors over $\mathcal C$ .

This definition is a convenient way of remembering the axioms of a monad: they’re the same as a monoid. To be more explicit: a monad is a functor $T:\mathcal C\to\mathcal C$ endowed with a unit $\eta:(-)\Rightarrow T$ and a multiplication $\mu:T\circ T\Rightarrow T$ such that the unit acts by identity under multiplication, and multiplication is associative.

Even though the axioms themselves aren’t too challenging, monads can be an incredibly difficult concept to digest, since it really puts your ability to think abstractly on the spot. Sure, a monoid is easy enough (a set with an associative, unital multiplication), but for a monad, you replace the set with a functor! What’s a good way to think about monads then? Well, don’t quote me, but for the purposes of this post at least, this should be sufficient:

If $X$ is an object (viewed as a set of things) of the category $\mathcal C$ and $T$ is a monad, then $TX$ can be thought of as the object of certain “constructions” performed formally (formal = no “real world” considerations; that is, done freely) on $X$ . The unit map $\eta_X:X\to TX$ reflects how everything “real” in $X$ can be viewed as “formal,” and the multiplication map $\mu_X:TTX\to TX$ reflects how anything that is “formally formal” is just “formal.”

To see what I mean, consider a few examples:

The Kleene star monad over sets
- This takes a set $X$ and gives the collection of all finite lists of elements of $X$ ; that is, $\displaystyle X^* = \bigcup_{n\geq0}X^n = \left\{(x_1,\dots,x_n) \middle| \substack{x_1,\dots,x_n\in X \\ n\geq0}\right\}$
- The monad unit realises every element $x\in X$ as the one-element list $(x)\in X^*$
- The monad multiplication takes a list of lists and concatenates them all as a single list: for example $((x_1,x_2),(x_3),(x_4,x_5)) \mapsto (x_1,x_2,x_3,x_4,x_5)$ .
The “free -module” monad over sets
- This takes a set $X$ and gives the collection of all formal $R$ -linear combinations of elements of $X$ ; that is, $\displaystyle \mathrm{Span}_RX := \left\{\sum_{i=1}^nr_ix_i \middle| \substack{r_1,\dots,r_n\in R \\ x_1,\dots,x_n\in X \\ n\geq0}\right\}$ (modulo obvious relations like $r_1x_1 + r_2x_1 = (r_1+r_2)x_1$ )
- The monad unit realises every element $x\in X$ as the trivial formal linear combination $1\cdot x\in\mathrm{Span}_RX$ .
- The monad multiplication observes that a formal linear combination of formal linear combinations can be made into just a one-step formal linear combination: for example $r_1(s_1x_1+s_2x_2) + r_2(s_3x_1+s_4x_4) \mapsto (r_1s_1+r_2s_3)x_1 + r_1s_2x_2 + r_2s_4x_4$ .
The group algebra monad over groups
- This takes a group $G$ and gives the collection of all formal $R$ -linear combinations of elements of $G$ as above, but with multiplication induced by the multiplication of group elements. More precisely, $R[G]$ is the module $\mathrm{Span}_RG$ where the multiplication is given by $\displaystyle \left(\sum_{i=1}^nr_ig_i\right)\left(\sum_{j=1}^ms_jh_j\right) = \sum_{i=1}^n\sum_{j=1}^m(r_is_j)(g_ih_j)$ .
- The monad unit and multiplication are as before.
The maybe monad on sets (or types)
- This takes a type and returns a type that is extended to include an “error” instance (at least, this is the interpretation). This means that a function whose output type is $\mathrm{Maybe}(X)$ either produces an element of $X$ , or throws an error. Mathematically, the monad is very simple: it is $\mathrm{Maybe}(X) = X\sqcup\{*\}$ (where the new element is the “error” element).
- The monad unit just observes that the type is extended: everything in the original type is still there.
- The monad multiplication merges two “error” elements to be the same thing; that is, it is the projection $X\sqcup\{*_1,*_2\}\to X\sqcup\{*\}$ sending both $*_1,*_2\mapsto*$ .
For a weird example (i.e., stretches the interpretation I gave): the abelianisation monad over groups
- This takes a group $G$ and gives the abelianisation $G^{\mathrm{ab}} = G/[G,G]$ , which is the result of forcing all elements of $G$ to commute.
- The monad unit is the canonical projection $G\to G^{\mathrm{ab}}$ , sending every group element to itself in the abelianisation.
- The monad multiplication in this case is actually an isomorphism $(G^{\mathrm{ab}})^{\mathrm{ab}}=G^{\mathrm{ab}}$ . It says that nothing changes if you abelianise a group that is already abelian.

Notice that “formal” and “free” mean very similar things (at least mathematically). This is no mere coincidence. In some sense, any pair of adjoint functors can be thought of as a free-forgetful adjunction (see, for instance, an older post), and…

Observation 2. Given an adjoint pair of functors $L:\mathcal C\leftrightarrows\mathcal D:R$ , the composite $RL$ canonically defines a monad on $\mathcal C$ . The unit is precisely the adjunction unit $\eta:(-)\Rightarrow RL$ , and the multiplication is induced by the counit: $\mu=R\epsilon_L:RLRL\Rightarrow RL$ .

In fact, all of the above examples come from an adjoint pair:

The Kleene star comes from the forgetful functor $\mathbf{Mon}\to\mathbf{Set}$ , with left adjoint the “free monoid” functor. Hence, the Kleene star is sometimes referred to as the “free monoid” monad.
The “free $R$ -module” monad comes, unsurprisingly, from the forgetful functor $R\mathbf{Mod}\to\mathbf{Set}$ , being the left adjoint.
The group $R$ -algebra construction comes from the “group of units” functor $(-)^\times:R\mathbf{Alg}\to\mathbf{Grp}$ , being the left adjoint.
The maybe monad comes as left adjoint to the forgetful functor $\mathbf{Set}_*\to\mathbf{Set}$ from pointed sets.
The abelianisation monad comes as left adjoint to the forgetful functor $\mathbf{Ab}\to\mathbf{Grp}$ .

This, too, is no coincidence. Every monad comes from an adjoint pair! In fact, although adjoint functors can be viewed as free-forgetful pairs in a loose sense, monads can be viewed as monads of free-forgetful adjunctions in a much more precise way.

Algebras of a monad

Let $T$ be a monad over a category $\mathcal C$ . If we want to realise this as the “free/formal structures” monad coming from an adjunction, then we need a category whose objects are those of $\mathcal C$ equipped with the structure that $T$ is allegedly building formally. This is achieved by the $T$ –algebras:

Definition 3. An algebra over $T$ is an object $X$ equipped with an “action” $\alpha:TX\to X$ such that the unit acts by identity (meaning $X\xrightarrow{\eta_X}TX\xrightarrow{\alpha}X$ is the identity), and the action of a multiplication coincides with iterated action (meaning $TTX\xrightarrow{\mu_X}TX\xrightarrow{\alpha}X$ is the same as $TTX\xrightarrow{T\alpha}TX\xrightarrow{\alpha}X$ ).

Intuitively, the action in a $T$ -algebra encodes a way of realising the “formal” constructions of $TX$ as truly living in $X$ . The category of all $T$ -algebras (and action-preserving morphisms) is the Eilenberg-Moore category $\mathcal C^T$ .

An algebra $(X,\alpha)$ of the Kleene star monad is precisely a monoid, with the action defining the (multiary) multiplication. In particular, the binary product is given by $x\cdot y =: \alpha(x,y)$ , and the monoid unit is given by the empty list $1_X =: \alpha()$ . The monad multiplication ensures that this product is associative and unital, while the unit ensures that the unary product doesn’t do anything: $\alpha(x)=x$ . Therefore, the Eilenberg-Moore category of the Kleene star is the category of monoids $\mathbf{Set}^{(-)^*}=\mathbf{Mon}$ .
An algebra of the free $R$ -module monad is exactly an $R$ -module, since it realises a formal linear combination as a true element. Therefore, the Eilenberg-Moore category is the category of modules $\mathbf{Set}^{\mathrm{Span}_R}=R\mathbf{Mod}$ .
An algebra of the group algebra construction is just a group algebra. $\mathbf{Grp}^{R[-]}=R\mathbf{Alg}$ .
An algebra of the maybe monad is a pointed set. The action absorbs the “error” state into the distinguished element. $\mathbf{Set}^{\mathrm{Maybe}}=\mathbf{Set}_*$ .
An algebra of the abelianisation is, surprisingly (to me), an abelian group. Indeed, the abelianisation unit (i.e., projection) is already surjective, and the action of an algebra has to be a retraction of the unit. This forces the unit to be bijective and thus an isomorphism of groups. $\mathbf{Grp}^{(-)^{\mathrm{ab}}}=\mathbf{Ab}$ .

There is an obvious forgetful functor $U:\mathcal C^T\to\mathcal C$ just given by forgetting the action, and the “free $T$ -algebra” left adjoint is also not hard to construct. In fact, it is given by $T$ : for any object $X$ , the object $TX$ has a tautological action given by the monad multiplication $\mu_X:T(TX)\to TX$ .

Monadicity

Although all monads come from adjunctions, the converse is false. Given an arbitrary adjunction $L:\mathcal C\leftrightarrows\mathcal D:R$ , we certainly get a canonical functor $\mathcal D\to\mathcal C^{RL}$ (induced by $R$ , and this is in fact the unique such functor that respects the “forgetful” functors to $\mathcal C$ ), but it need not be an equivalence. In the case that it is an equivalence, the adjunction (or, for brevity and convenience, just the right adjoint) is said to be monadic. For example, we have shown that: monoids are monadic over sets, ring modules are monadic over sets, group algebras are monadic over groups, pointed sets are monadic over sets, and abelian groups are monadic over groups.

For a simple non-example, just take the category of topological spaces and its forgetful functor $\mathbf{Top}\to\mathbf{Set}$ . The left adjoint is the “discrete space” functor, but the induced monad is then just the identity monad on $\mathbf{Set}$ . Therefore, topological spaces are not monadic over sets. Comparing this adjunction to all of the above (monadic) adjunctions, you might infer an intuition about monadicity: adjunctions tend to be monadic if they come from forgetting algebraic structure.

Note. Magically, if you restrict topological spaces to compact Hausdorff spaces, then you recover monadicity! More precisely, the forgetful functor $\mathbf{CHaus}\to\mathbf{Set}$ admits a left adjoint (given by the Stone-Čech compactification on the set viewed as a discrete space). For a discrete space $X$ , the compactification is given by taking the set of ultrafilters on $X$ (the topology on $\beta X$ is generated by sets of the form $\{F\in\beta X \mid U\in F\}$ for $U\subseteq X$ ). The action of a $\beta$ -algebra assigns to an ultrafilter (think: Cauchy “sequence”) a point (think: limit point) of $X$ , so ultimately induces a compact Hausdorff topology on $X$ . This ultimately shows that $\mathbf{Set}^\beta=\mathbf{CHaus}$ .

So how do we know if a functor is monadic? I mean, besides constructing the Eilenberg-Moore category for the induced monad and hoping that the forgetful functor factors via equivalence through it.

Luckily, there is a more concrete way of verifying this.

Theorem 4 (Beck’s monadicity theorem). [Bor94(II), Thm 4.4.4] A functor $R:\mathcal D\to\mathcal C$ is monadic if and only if

$R$ admits a left adjoint $L$
$R$ creates coequalisers of $R$ -split pairs (these are pairs of morphisms whose images under $R$ admits a split coequaliser)

Proof. One direction is easier than the other. If $R$ is monadic, then without loss of generality, write $R=U$ with left adjoint $T$ , and write $\mathcal D=\mathcal C^T$ . Suppose $f,g:(X,\alpha)\to(Y,\beta)$ make a $U$ -split pair. This means that we have morphisms as in the diagram

such that $e\circ s=\mathrm{id}_Z$ and $f\circ r=\mathrm{id}_Y$ are sections, and $g\circ r=s\circ e$ is idempotent. This gives $Z$ canonical $T$ -algebra structure: the action is given by $TZ\xrightarrow{Ts}TY\xrightarrow{\beta}Y\xrightarrow{e}Z$ . This works because split equalisers are universal (i.e., preserved by all functors) and are in particular preserved by $T$ and $TT$ , which ensures that this action respects the unit and multiplication of $T$ (see [Bor94(II), Prop 4.3.2] for a detailed proof).

More interesting is the converse. We aim to prove that the induced functor $R:\mathcal D\to\mathcal C^T$ (for $T=RL$ ) is an equivalence. If you let $\mathcal C_T\subseteq\mathcal C^T$ denote the full subcategory of free $T$ -algebras (i.e., the Kleisli category), then we have a canonical map $\mathcal C_T\to\mathcal D$ given by sending $TX=RLX\mapsto LX$ (which is well-defined by the zigzag identities), and the composite $\mathcal C_T\to\mathcal D\to\mathcal C^T$ is precisely the full inclusion. Therefore, $R:\mathcal D\to\mathcal C^T$ is full.

Let $(X,\alpha)$ be a $T$ -algebra, then the pair $\epsilon_{LX},L\alpha:LRLX\rightrightarrows LX$ is $R$ -split (under $R$ , this pair becomes $\mu_X,T\alpha:TTX\rightrightarrows TX$ , which has coequaliser $X$ , and the adjunction unit as both sections). Thus, by assumption, we can construct a coequaliser in $\mathcal D$ , and preservation ensures that the image of this colimit under $R$ is precisely $(X,\alpha)$ in $\mathcal C^T$ .

To see that $R:\mathcal D\to\mathcal C^T$ is faithful (completing the proof), it suffices to prove that the adjunction counit is an epimorphism. This is because the zigzag identities make the pair $\epsilon_{LRX},LR\beta_X:LRLRX\rightrightarrows LRX$ out to be $R$ -split, and the image under $R$ has coequaliser $RX$ , therefore lifting to a coequaliser $LRLRX\rightrightarrows LRX\xrightarrow{\epsilon_X}X$ , as desired. $\blacksquare$

Why monads?

Rather than “why monads,” the better question is probably “why monadicity?” I’m sure monads themselves have many useful properties (that I have not yet seen), but monadicity can be convenient. The most evident advantage is that monadicity of $\mathcal D$ over a category $\mathcal C$ allows you to reason with the objects of $\mathcal D$ as structured objects of $\mathcal C$ in a very precise sense (in fact, the structure even algebraic in a way). This is particularly useful when working with categories that are monadic over sets.

Through this, one can hope to lift many properties of $\mathcal C$ to the monadic category. For example, general forgetful functors (i.e., right adjoints) preserve limits, but monadic functors create limits. On the other hand, the forgetful functor reflects any colimit that is preserved by the monad. If $\mathcal C$ is cocomplete, then so is $\mathcal C^T$ once it has reflexive coequalisers (in particular, every monadic category over sets is complete and cocomplete).

Related to this, we can also hope to lift adjunctions through monadic functors.

Theorem 4 (Adjoint triangle theorem). [SV10, Lemma 2.1] Suppose $F:\mathcal C\leftrightarrows\mathcal B:U$ is an adjoint pair such that the adjunction counits are all regular epimorphisms (i.e., coequaliser maps; in fact, it is equivalent to asserting that the diagrams $\epsilon_{FUB},FU\epsilon_B:FUFUB\rightrightarrows FUB\xrightarrow{\epsilon_B}B$ are coequaliser diagrams. Since the parallel arrows have a common section given by the unit $F\eta_{UB}$ , these are reflexive coequalisers). Note that this condition is met by any monadic functor $U:\mathcal B\to\mathcal C$ .

If $\mathcal A$ is a category with all reflexive coequalisers, then a functor $R:\mathcal A\to\mathcal B$ has a left adjoint if and only if $UR:\mathcal A\to\mathcal C$ does, as in the picture

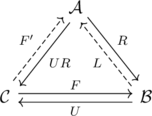
Proof. Adjunctions are closed under composition, so one direction is clear. Suppose we have a left adjoint $F'\dashv UR$ , then we wish to construct a left adjoint of $R$ . By assumption, every counit map arises from a relfexive coequaliser $FUFUB\rightrightarrows FUB\xrightarrow{\epsilon_B}B$ . Therefore, the left adjoint is defined on any $B\in\mathcal B$ as the (reflexive) coequaliser $F'UFUB\rightrightarrows F'UB\to LB$ . To see why this works, apply several adjunctions:

where every row is a (reflexive) equaliser, applying the Yoneda lemma. $\blacksquare$

As a corollary, we get the more convenient result:

Theorem 5 (Adjoint lifting theorem). Suppose $\mathcal A$ is monadic over $\mathcal C$ , and $\mathcal B$ is monadic over $\mathcal D$ . Let $Q:\mathcal A\to\mathcal B$ and $R:\mathcal C\to\mathcal D$ fit in the commutative square

If $\mathcal A$ has reflexive coequalisers and $R$ has a left adjoint, then $Q$ admits a left adjoint as well.

Proof. Draw the diagonal functor $VQ:\mathcal A\to\mathcal D$ . Since $VQ=RU$ and the latter has left adjoints, we easily get a left adjoint to $VQ$ . Therefore, by the adjoint triangle theorem applied to the upper-right triangle, $Q$ has a left adjoint as well. $\blacksquare$

Monadicity in action

The application which led me to want to spell out all of this stuff is the following result (which surprised me at first, but perhaps that just exposes my naïvité). Suppose $(\mathcal V,\otimes,\mathbb I)$ is a monoidal category, and we have another (small, I guess) category $\mathcal I$ . Then, we can endow the functor category $\mathrm{Fun}(\mathcal I,\mathcal V)$ with monoidal structure just by having the tensor product act pointwise. This is unsurprising, and what else is unsurprising is that the pointwise tensor product inherits many basic properties of the original one: being braided, symmetric, cartesian (thanks to limits being computed pointwise), etc.

What came as a surprise to me is that the pointwise tensor product inherits (right) closedness as well (under suitable conditions on $\mathcal V$ )! Recall that a monoidal category is (right) closed if tensoring from the right admits a right adjoint: $(-)\otimes v\dashv[v,-]$ for every $v\in\mathcal V$ , which is called the internal hom. Naïvely, to endow the functor category with an internal hom, one might try to perform it pointwise: set $[F,G](I) := [F(I),G(I)]$ for $F,G:\mathcal I\to\mathcal V$ and $I\in\mathcal I$ . However, this construction is not functorial: internal homs, like ordinary homs, are contravariant in the first variable. This is only successful if the domain category $\mathcal I$ were discrete, so that there is no action of morphisms to consider.

Nonetheless, we have the following result:

Proposition 6. If $\mathcal V$ is a complete (right) closed monoidal category, and $\mathcal I$ is small, then $\mathrm{Fun}(\mathcal I,\mathcal V)$ is closed monoidal under the pointwise tensor product.

Proof. Let $i:\mathcal I_0\hookrightarrow\mathcal I$ be the canonical inclusion of the discrete subcategory spanned by the objects of $\mathcal I$ . Since $\mathcal V$ is complete, the induced map $i^*:\mathrm{Fun}(\mathcal I,\mathcal V)\to\mathrm{Fun}(\mathcal I_0,\mathcal V)$ admits a right adjoint $\mathrm{Ran}_i=i_*:\mathrm{Fun}(\mathcal I_0,\mathcal V)\to\mathrm{Fun}(\mathcal I,\mathcal V)$ given by the (discrete) right Kan extension

$\displaystyle i_*(F_0)(I) := \int_{J\in\mathcal I_0}\prod_{\mathrm{Hom}_{\mathcal I}(I,J)}F_0(J) = \prod_{I\to J}F_0(J)$

Note that since both functor categories are complete, with limits computed pointwise, it follows that $i^*:\mathrm{Fun}(\mathcal I,\mathcal V)\to\mathrm{Fun}(\mathcal I_0,\mathcal V)$ creates all limits, and so we may apply (the dual of) Beck’s monadicity theorem to conclude that $i^*$ is comonadic. Therefore, (the dual of) the adjoint lifting theorem ensures that the right adjoint of every functor $(-)\otimes i^*F:\mathrm{Fun}(\mathcal I_0,\mathcal V)\to\mathrm{Fun}(\mathcal I_0,\mathcal V)$ (which we already know exists, given by pointwise internal hom) lifts to a right adjoint to the functor $(-)\otimes F:\mathrm{Fun}(\mathcal I,\mathcal V)\to\mathrm{Fun}(\mathcal I,\mathcal V)$ for every $F:\mathcal I\to\mathcal V$ . $\blacksquare$

Remark. $\mathrm{Fun}(\mathcal I,\mathcal V)$ is also monadic over $\mathrm{Fun}(\mathcal I_0,\mathcal V)$ via the (discrete) left Kan extension. The proof is the same: both categories are cocomplete with pointwise colimits, so Beck’s monadicity theorem applies.

But what does the internal hom look like? This is what motivated the post.

The most systematic way of working it out is to just retrace the relevant proofs and hope it gives a legible formula. First, the main ingredient: the adjoint triangle theorem. Using the notation as in the theorem:

Assuming that the left adjoint $F'$ exists, then the functor $L$ was defined pointwise on $B\in\mathcal B$ as the coequaliser of the maps

$F'UFUB \xrightarrow{F'U\epsilon_B}F'UB$ and $F'UFUB \xrightarrow{F'U\theta_{UB}}F'URF'UB\xrightarrow{\epsilon'_{F'UB}}F'UB$

where $\theta_C:FC\xrightarrow{F\eta'_C}FURF'C\xrightarrow{\epsilon_{RF'C}}RF'C$ .

In our case, we need to apply this dually (though hopefully once is sufficient, since the forgetful functor just forgets the actions of morphisms and leaves the objects unchanged). Fix a functor $F:\mathcal I\to\mathcal V$ , so the goal is to construct the right adjoint to $(-)\otimes F$ . Just as in the proof of the adjoint functor theorem, a right adjoint to the composite functor $i^*(-\otimes F):\mathrm{Fun}(\mathcal I,\mathcal V)\to\mathrm{Fun}(\mathcal I_0,\mathcal V)$ is right at hand since $i^*(-\otimes F)=i^*(-)\otimes F_0\dashv i_*[F_0,-]$ , where $F_0=i^*F$ and $[F_0,-]$ is the pointwise internal hom in $\mathrm{Fun}(\mathcal I_0,\mathcal V)$ .

Therefore, the right adjoint to $(-)\otimes F$ is given by a (pointwise) equaliser

$\displaystyle [F,G] \to i_*[F_0,G_0] \rightrightarrows i_*[F_0,i^*i_*G_0]$

The first arrow comes from the adjunction unit $\eta_G:G\Rightarrow i_*G_0$ given by the evident map $G(I)\to\prod_{I\to J}G_0(J)=\prod_{I\to J}G(J)$ . The other map comes from the mate $\theta_{G_0}:i_*[F_0,G_0]\otimes F\Rightarrow i_*G_0$ given by the evident map $\left(\prod_{I\to J}[F(J),G(J)]\right)\otimes F(I)\to\prod_{I\to J}G(J)$ . In summary, for every $I\in\mathcal I$ , the internal hom is the equaliser

$\displaystyle [F,G](I) \to \prod_{I\to J}[F(J),G(J)]\rightrightarrows\prod_{I\to J\to K}[F(J),G(K)]$

Intuitively, the middle object collects morphisms $f_\varphi:F(J)\to G(J)$ for every $\varphi:I\to J$ , and the upper arrow maps this family to the family of $\psi_*\circ f_\varphi:F(J)\to G(J)\to G(K)$ for every $I\xrightarrow\varphi J\xrightarrow\psi K$ , while the lower arrow maps this family to the family of $f_{\psi\varphi}\circ\psi_*:F(J)\to F(K)\to G(K)$ for every $I\xrightarrow\varphi J\xrightarrow\psi K$ .

In particular, if you let $f_I := f_{\mathrm{id}_I}:F(I)\to G(I)$ , then diagrammatically, the elements of $[F,G](I)$ are given by a choice of $f_I:F(I)\to G(I)$ along with a chosen extension $f_\varphi:F(J)\to G(J)$ for every $\varphi:I\to J$ such that for any $I\xrightarrow\varphi J\xrightarrow\psi K$ , we have commutativity of the diagram

In other words, the internal hom evaluated at $I$ gives partial information about natural transformations $F\Rightarrow G$ that are possible, as can be “seen” from mapping out of $I$ . Moreover, we can see how this construction is functorial: if $\phi:I\to J$ , then the map $[F,G](I)\to[F,G](J)$ just restricts families via the intuitive formula $\{f_\varphi:F(K)\to G(K)\}_{\varphi:I\to K}\mapsto\{f_{\psi\phi}:F(K)\to G(K)\}_{\psi:J\to K}$ . In particular, a true natural transformation $F\Rightarrow G$ would be built up from the morphisms $f_I:F(I)\to G(I)$ as in the above diagram (naturality of this choice then following from the functoriality of $[F,G]$ ).

I can see why I couldn’t find an explicit formulation of the internal hom for the pointwise tensor product, but this formula is actually surprisingly satisfactory and concrete (literally, the intuition can be made precise if $\mathcal V$ is a concrete category).