The nerve to be so dense

I mentioned in an old post that any “shape” functor $S:\mathcal S\to\mathcal C$ into a cocomplete category $\mathcal C$ induces a nerve-realisation adjunction $|-|:\mathbf{PSh}(\mathcal S)\rightleftarrows\mathcal C:N$ , where the right adjoint is given by $N_X(s) := \mathrm{Hom}_{\mathcal C}(S(s),X)$ .

Perhaps the prototypical example of this phenomenon is in the context of the geometric realisation of simplicial sets. Here, we take $\mathcal S := \Delta$ to be the simplex category, and $S:\Delta\to\mathbf{Top}$ realises the $n$ -simplex as the topological space

$\Delta_{\mathbf{Top}}[n] := \{(x_0,\dots,x_n)\in\mathbb{R}^{n+1}_{\geq0} \mid x_0+\dots+x_n=1\}$

The left adjoint is then the geometric realisation $|-|:\mathbf{sSet}\to\mathbf{Top}$ of simplicial sets as topological spaces (obtained by gluing the above topological simplices together according to the construction of the corresponding simplicial set), and the right adjoint sends a space $X$ to the complex of singular simplices in $X$ . As mentioned in the old post, this adjunction is far from a genuine equivalence: the singular complex only defines a full faithful embedding of the discrete topological spaces. However, if you only care about the homotopical structure of topological spaces (i.e., the canonical $(\infty,1)$ -categorical structure), then the above adjunction becomes a full-fledged equivalence of $(\infty,1)$ -categories, meaning that at this level, we can simplify the study of topological spaces dramatically by studying the (easier) category of simplicial sets.

The example I was more interested in that old post was if we take the canonical inclusion $\mathbf{Op}(X)\to(\mathbf{Top}\downarrow X)$ of open subsets of a space $X$ into the category of spaces lying over $X$ . In this context, the nerve induces a fully faithful embedding of étale spaces over $X$ whose essential image is precisely the subcategory of sheaves on $X$ .

Recall that a space $Y$ lying over $X$ is étale if the projection $Y\to X$ is a local homeomorphism; that is, every $y\in Y$ admits an open neighbourhood $V\ni y$ for which $f|:V\to f(V)$ is a homeomorphism into an open subset of $X$ . In particular, this means inclusions of open subsets $U\hookrightarrow X$ are local homeomorphisms, so we really have a canonical inclusion $\mathbf{Op}(X)\hookrightarrow\mathbf{\acute Et}(X)$ , and the induced nerve $\Gamma:\mathbf{\acute Et}(X)\to\mathbf{PSh}(\mathbf{Op}(X))$ is fully faithful.

What’s so special about the realisation of open subsets as étale that allows us to embed all étale spaces into presheaves on $X$ , as compared to the realisation of open subsets as a general topological space over $X$ , or compared to the realisation of simplices as topological spaces? Recall that Proposition 2 from the same old post tells us that a right adjoint is fully faithful iff the adjunction counit is a natural isomorphism. This means that a nerve is fully faithful iff $|N_Y|\to Y$ is an isomorphism for every $Y\in\mathcal C$ .

In the old post (near the bottom), I explained how $Y$ being étale over $X$ is equivalent to $|\Gamma_{Y/X}|\to Y$ being a homeomorphism, but here I will explain it using a more sophisticated point of view. Notice that inclusions of open sets $U\to X$ are almost tautologically local homeomorphisms (I mean, for any point $x\in U$ , you can just use $U$ as the open neighbourhood of $x$ for which the inclusion is homeomorphic to its image). On the other hand, you can equivalently think of local homeomorphisms as the results of patching together a bunch of inclusions of open sets of $X$ . In fact, this is exactly what $|\Gamma_{Y/X}|$ is:

$\displaystyle |\Gamma_{Y/X}| = \int^{U\subseteq X}\coprod_{\Gamma_{Y/X}(U)}U$

We get a copy of the inclusion $U\hookrightarrow X$ for every local section of $Y\to X$ defined on $U$ , and they get patched together according to how the images of these sections overlap in $Y$ . For this to recover $Y$ , we need that (sufficiently small) local sections map homeomorphically back into $Y$ , which is precisely what it means for $Y$ to be étale.

Phrased differently, we have just proven that étale spaces are precisely those spaces that can be written as a particular colimit of inclusions of open subsets, and this is why the nerve corresponding to the inclusion $\mathbf{Op}(X)\to\mathbf{\acute Et}(X)$ is fully faithful. Since colimits are the categorical analogue of topological limits (I know, great terminology), we could say that $\mathbf{Op}(X)$ is dense in $\mathbf{\acute Et}(X)$ .

If we want to think about this phenomenon (and its relation to nerves) more generally, we need to be more precise about what this sort of density means. In particular, we should be more precise about the colimit exhibiting $|\Gamma_{Y/X}|$ : the coend of a coproduct is a bit clunky, and takes advantage of the cocompleteness of $\mathbf{\acute Et}(X)$ .

For a general shape functor $S:\mathcal S\to\mathcal C$ , the universal property exhibiting $|N_X|$ as a coend for $X\in\mathcal C$ is as follows: for any $s\in\mathcal S$ , we have a canonical map $\coprod_{N_X(s)}S(s)\to|N_X|$ , and given any $s\to s'$ in $\mathcal S$ , the corresponding compositions

$\displaystyle \coprod_{N_X(s')}S(s) \to \coprod_{N_X(s)}S(s) \to |N_X|$

$\displaystyle \coprod_{N_X(s')}S(s) \to \coprod_{N_X(s')}S(s')\to |N_X|$

are equal. Since we are interested in when the nerve is fully faithful, the counit $|N_X|\to X$ needs to be an isomorphism, so the universal property may be stated directly for $X$ . In this case, the canonical maps $\coprod_{N_X(s)}S(s)\to X$ are given by cotupling the maps $S(s)\to X$ in $N_X(s)=\mathrm{Hom}_{\mathcal C}(S(s),X)$ , and $X$ needs to be universal with such maps. More precisely, if we have some object $Y$ such that we have a map $S(s)\to Y$ for every map $S(s)\to X$ , and this family is compatible with all $s\to s'$ in $\mathcal S$ , then there must exist a unique $X\to Y$ which factors each $S(s)\to X$ through the correspondinge $S(s)\to Y$ . This is to say that the canonical map

$\displaystyle \varinjlim\left((S\downarrow X)\xrightarrow{\mathrm{proj}}\mathcal S\xrightarrow S\mathcal C\right) \to X$

is an isomorphism, where $(S\downarrow X)$ is the comma category whose objects are pairs $(s,S(s)\to X)$ and whose morphisms are those $s\to s'$ for which $S(s)\to S(s')$ lies over $X$ . In particular, the above map is an isomorphism is equivalent to saying that $|N_X|\to X$ is an isomorphism, which is then equivalent to saying that $N:\mathcal C\to\mathbf{PSh}(\mathcal S)$ is fully faithful. The benefit of this incarnation is that it is solely a property of the functor $S:\mathcal S\to\mathcal C$ .

Note that this also eliminates the need of cocompleteness in $\mathcal C$ . Indeed, recall that the cocompleteness of $\mathcal C$ is only necessary for extending $S:\mathcal S\to\mathcal C$ to the realisation functor (i.e., the left adjoint) $|-|:\mathbf{PSh}(\mathcal S)\to\mathcal C$ . Indeed, this is exactly the 2-universal property of $\mathbf{PSh}(\mathcal S)$ as the free cocompletion of $\mathcal S$ . However, the nerve right adjoint has a very simple formula $N_X(s) := \mathrm{Hom}_{\mathcal C}(S(s),X)$ that is well-defined for any category $\mathcal C$ . Likewise, replacing the coend condigion $|N_X|\cong X$ with the statement that $X$ is a canonical colimit definable solely in terms of $S$ , and therefore also eliminates the need for cocompleteness of $\mathcal C$ .

Theorem 1. For an arbitrary functor $\mathcal S\to\mathcal C$ , the following are equivalent (and any functor satisfying either property is called dense):

The functor $N:\mathcal C\to\mathbf{PSh}(\mathcal S)$ given by $N_X(s) := \mathrm{Hom}_{\mathcal C}(S(s),X)$ is fully faithful
Any $X\in\mathcal C$ is the colimit $\varinjlim\left((S\downarrow X)\to\mathcal S\xrightarrow S\mathcal C\right)$ .

Proof. Suppose we have for every $\varphi:S(s)\to X$ some map $\phi_\varphi:S(s)\to Y$ such that

This is exactly what it means for $\phi$ to define a natural transformation $\mathrm{Hom}_{\mathcal C}(S(-), X)\Rightarrow\mathrm{Hom}_{\mathcal C}(S(-),Y)$ via $\varphi\mapsto\phi_\varphi$ . By definition, this is a natural transformation $\phi:N_X\Rightarrow N_Y$ . Therefore, we get that this corresponds to a unique compatible morphism $X\to Y$ iff $N$ is fully faithful. $\blacksquare$

We get a couple interesting corollaries:

Take $\mathcal C=\mathcal S$ and $S$ the identity functor. Certainly $X=\varinjlim_{Y\to X}Y$ so that this functor is dense by criterion 2 of the theorem. The corresponding nerve $\mathcal C\to\mathbf{PSh}(\mathcal C)$ sends $X\mapsto\mathrm{Hom}_{\mathcal C}(-,X)$ —this is the Yoneda embedding $X\mapsto h_X$ . Therefore, Theorem 1 proves that the Yoneda embedding is fully faithful as a special case, and so can be thought of as a generalisation of this fact.
Now take and the Yoneda embedding. The corresponding nerve is given by . By the Yoneda Lemma, this means so that the nerve is the identity functor. By Theorem 1, this proves that every presheaf is a canonical colimit of representables.
- In fact, since $\mathbf{PSh}(\mathcal S)$ is cocomplete, we also recover the co-Yoneda Lemma: since the identity functor is an equivalence, it follows that $A = |N_A| = \int^{s\in\mathcal S}\coprod_{A(s)}h_s$ . Keep in mind that all of this relies on having already established the Yoneda Lemma.

The first corollary—fully faithfulness of the Yoneda embedding—is typically given as a consequence of the Yoneda Lemma, so this suggests that Theorem 1 may be a consequence of a generalisation of the Yoneda Lemma. Recall that the Yoneda Lemma states that $\mathrm{Nat}(h_X,F) \cong F(X)$ , from which it’s immediate that $\mathrm{Nat}(h_X,h_Y) = h_Y(X) = \mathrm{Hom}_{\mathcal C}(X,Y)$ . In our case, we have instead, assuming density of $S:\mathcal S\to\mathcal C$ , that

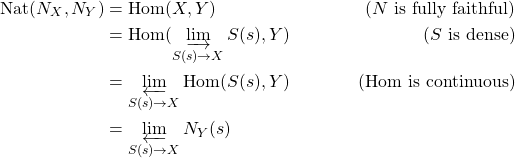
This formula readily allows us to substitute $N_Y$ out with any presheaf on $\mathcal S$ . This gives the following more elementary result:

Lemma 2. For an arbitrary functor $S:\mathcal S\to\mathcal C$ , we have that

$\displaystyle \mathrm{Nat}(\mathrm{Hom}(S(-),X),A) \cong \varprojlim_{S(s)\to X}A(s)$

naturally in objects $X\in\mathcal C$ and presheaves $A:\mathcal S^{\mathrm{op}}\to\mathbf{Set}$ .

Proof. An element of the limit on the right (which is computed in $\mathbf{Set}$ , which is why it’s enough to look at elements) is a choice of elements $a_\varphi\in A(s)$ for every $\varphi:S(s)\to X$ such that $A_j(a_\varphi) = a_{\varphi\circ S(j)} \in A(s)$ for every $j:s\to s'$ and $\varphi:S(s')\to X$ . This is exactly a natural transformation $a:\mathrm{Hom}(S(-),X)\Rightarrow A$ , completing the proof. $\blacksquare$

By taking $A := N_Y$ , Lemma 2 tells us that

$\displaystyle\mathrm{Nat}(N_X,N_Y) = \varprojlim_{S(s)\to X}N_Y(s) = \mathrm{Hom}(\varinjlim_{S(s)\to X}S(s),Y)$

And so $\mathrm{Nat}(N_X,N_Y) = \mathrm{Hom}(X,Y)$ for all $Y$ if and only if $\varinjlim_{S(s)\to X}S(s) = X$ , which is exactly the statement of Theorem 1. (Note that we don’t actually need the Yoneda Lemma anywhere here if we define colimits using homs.)

Now, we can derive the Yoneda Lemma immediately: just take $\mathcal C=\mathcal S$ and $S$ the identity functor, then Lemma 2 identifies $\mathrm{Nat}(h_X,A) = \varprojlim_{Y\to X}A(Y) = A(X)$ .

Weighing in on what our limits are

I was tempted to call Lemma 2 a “generalised Yoneda Lemma,” but perhaps Lemma 2 doesn’t exactly convey the same kind of message that the Yoneda Lemma does (actually, the more I think about it in terms of generalised elements like in my post about set theory, this does seem to say something about using $S$ to make sense of $X$ -shaped elements of a presheaf $A$ over $\mathcal S$ ). There is, however, an actual generalisation of the Yoneda Lemma (in fact, there are several) which occurs when the category is enriched in a Bénabou cosmos $\mathcal V$ .

Explicitly, given such a cosmos (i.e., a complete and cocomplete closed symmetric monoidal category), let $\mathcal C$ be a $\mathcal V$ -enriched category. We can then define the presheaf $\mathcal V$ -category $\mathbf{PSh}(\mathcal C)$ by taking the objects to be enriched functors $F:\mathcal C^{\mathrm{op}}\to\mathcal V$ (note that “opposite” makes sense only because the monoidal structure on $\mathcal V$ is symmetric), and whose hom- $\mathcal V$ -objects are given by

$\displaystyle \mathrm{Nat}(F,G) := \int_{X\in\mathcal C}[F(X),G(X)]$

where $[-,-]$ is the internal hom in $\mathcal V$ . We have a canonical Yoneda map $\mathcal C\to\mathbf{PSh}(\mathcal C)$ sending $X\mapsto h_X := \mathrm{Hom}_{\mathcal C}^{\mathcal V}(-,X)$ as before, but where the local morphisms

$\displaystyle \mathrm{Hom}(X,Y) \to \mathrm{Nat}(h_X,h_Y) = \int_{Z\in\mathcal C}[h_X(Z),h_Y(Z)]$

are induced by currying the composition maps

$h_Y(X)\otimes h_X(Z) = \mathrm{Hom}(X,Y)\otimes\mathrm{Hom}(Z,X) \to \mathrm{Hom}(Z,Y) = h_Y(Z)$ .

and the (strong) enriched Yoneda Lemma tells us that there is an isomorphism $\mathrm{Nat}(h_X,F) \cong F(X)$ natural in all objects $X\in\mathcal C$ and all presheaves $F:\mathcal C^{\mathrm{op}}\to\mathcal V$ .

Is there accordingly a generalisation of Lemma 2 to this enriched setting? If there is, we can’t state it in the same form: the right hand side computes a limit over the morphisms $S(s)\to X$ , but we don’t have the luxury of “morphisms” in enriched category theory. In fact, even the notions of co/limits become more intricate in this setting.

Let’s explore this nuance first. Suppose we have a functor $F:\mathcal J\to\mathcal C$ . The slick definition of a limit of $F$ is that it is a representing object for the presheaf $\varprojlim_j\mathrm{Hom}_{\mathcal C}(-,F(j))$ (warning: if you ever speak of representables, the Yoneda Lemma is at work to ensure uniqueness), and in principle these limits are easier to compute: co/limits in presheaf categories are computed pointwise, and co/limits of sets can be defined explicitly. If I have a functor $G:\mathcal J\to\mathbf{Set}$ , its limit is precisely the set of families of points $x_j\in G(j)$ that are compatible with the structure morphisms of $\mathcal J$ . Any such family is equivalently a natural transformation $x:\mathrm{const}_{\mathrm{pt}}\Rightarrow G$ so that $\varprojlim G = \mathrm{Nat}(\mathrm{const}_{\mathrm{pt}},G)$ .

More generally, the limit of $F:\mathcal J\to\mathcal C$ is then an object $\varprojlim F$ equipped with bijections

$\mathrm{Hom}_{\mathcal C}(X,\varprojlim F) \cong \mathrm{Nat}(\mathrm{const}_{\mathrm{pt}}, \mathrm{Hom}_{\mathcal C}(X,F))$

natural in $X$ . Entirely analogously, the colimit of $f:\mathcal J\to\mathcal C$ is an object $\varinjlim F$ equipped with bijections

$\mathrm{Hom}_{\mathcal C}(\varinjlim F,Y) \cong \mathrm{Nat}(\mathrm{const}_{\mathrm{pt}}, \mathrm{Hom}_{\mathcal C}(F,Y))$

natural in $Y$ , recalling that colimits in the first argument of the hom are sent to limits outside the hom.

The issue with translating this to the enriched setting is that there is no analogue of $\mathrm{const}_{\mathrm{pt}}$ in general: this functor serves to pick out elements of $\mathrm{Hom}_{\mathcal C}(X,F(j))$ for every $j$ ; that is, it’s a specification of cone morphisms from $X$ to $F$ (in the colimit case, it specifies cocones). As we have already mentioned, there is no way to specify “morphisms” in an enriched category.

You might think: for any enriched category $\mathcal C$ , we can obtain an underlying ordinary category by taking the hom-sets to be $\mathrm{Hom}_{\mathcal C}^{\mathbf{Set}}(X,Y) := \mathrm{Hom}_{\mathcal V}(\mathbb I,\mathrm{Hom}_{\mathcal C}^{\mathcal V}(X,Y))$ , where $\mathbb I$ is the tensor unit of $\mathcal V$ . Note that this is actually a really good way of recovering an ordinary category: it does exactly what you want for many cases we care about (like when $\mathcal{V}$ is given by $\mathbf{Set}$ , $\mathbf{Ab}$ , $R\mathbf{Mod}$ , $\mathbf{Cat}$ , etc.), and $[\mathbb I,-] \cong\mathrm{id}_{\mathcal V}$ , so the enriched analogue of this action “does nothing,” so this is the most canonical ordinary category you can obtain from an enriched one.

The (genuine) morphisms $X\to Y$ of the underlying category, by definition, are the $\mathbb I$ -shaped generalised elements of $\mathrm{Hom}_{\mathcal C}^{\mathcal V}(X,Y)$ , so one would naturally guess that the enriched analogue of $\mathrm{const}_{\mathrm{pt}}$ is $\mathrm{const}_{\mathbb I}$ . This would be great as a substitute, but there’s a catch…

This functor doesn’t exist in general!

Indeed, such a functor would have to be enriched, meaning that we would have to guarantee that there always exist morphisms $\mathrm{Hom}_{\mathcal J}^{\mathcal V}(j,j') \to [\mathbb I,\mathbb I]\cong\mathbb I$ in $\mathcal V$ (and moreover, these morphisms have to be analogues of “sending everything to the identity”), but this is only a guarantee if $\mathbb I$ is terminal (i.e., the monoidal structure of $\mathcal V$ is semicartesian).

But hold on: what is going on with concrete categories like $\mathbf{Ab}$ then? The tensor unit here is $\mathbb{Z}$ , which is definitely not terminal, but we still have no trouble working with ordinary co/limits of e.g. abelian categories. Don’t be too hasty in saying that this is fine because $\mathbf{Ab}$ has zero morphisms: these are not the morphisms you want for the “constant functor” on $\mathbb{Z}$ (remember: these morphisms have to be constant on the identity of $\mathbb{Z}$ ). There’s actually a handful of stuff going on that makes this work.

First, these co/limits are over ordinary diagrams. This means that the diagrams are ordinary categories, so we need to canonically lift these to enriched categories first before we can talk about enriched co/limits. Since the enriching category is cocomplete, we can do this freely: given any set $T$ , identify it with the coproduct $\coprod_T\mathrm{pt}$ , then this suggests that the natural analogue of this set in $\mathcal V$ is $\coprod_T\mathbb I$ . This is functorial in $T$ , and the closed monoidal structure of $\mathcal V$ makes this construction (strongly) monoidal as well.

In more fancy language, existence of coproducts makes $\mathcal V$ copowered over $\mathbf{Set}$ , and we are sending $T$ to the copower $T\odot\mathbb I$ , which has a universal property similar to currying: $\mathrm{Hom}_{\mathcal V}(T\odot\mathbb I,X) \cong \mathrm{Hom}_{\mathbf{Set}}(T, \mathrm{Hom}_{\mathcal V}(\mathbb I,X))$ .

In particular, we can lift an ordinary category $\mathcal J$ to a “freely enriched” category $\mathcal J^{(\mathcal V)}$ . In particular, the freely enriched category on the terminal category $\mathbf1$ is the category $\mathbf1^{(\mathcal V)} = \mathbf{B}\mathbb I$ with one object and a hom-object given by $\mathbb I$ . Therefore, the constant functor $\mathrm{const}_{\mathrm{pt}}$ on $\mathcal J$ lifts to a corresponding functor

$\mathrm{const}_{\mathbb I}:\mathcal J^{(\mathcal V)} \to \mathbf1^{(\mathcal V)} = \mathbf{B}\mathbb I\subset\mathcal V$

With this construction, the limits we obtain are just enriched versions of ordinary limits: an enriched functor $F:\mathcal J^{(\mathcal V)}\to\mathcal C$ is exactly an ordinary functor from $\mathcal J$ to the underlying ordinary category of $\mathcal C$ , and if the enriched limit exists, then it coincides with the ordinary limit of $\mathcal F$ . For this reason, such limits are called conical. In particular, this is more of a pedestrian enriched limit: it does not even handle a genuine enriched functor $F:\mathcal J\to\mathcal C$ (with $\mathcal J$ an enriched category).

For general enriched functors, we don’t have a canonical substitute for $\mathrm{const}_{\mathbb I}$ , so we just make a choice of a “substitute” and make it part of the data. The choice of substitute is then called the weight:

Definition 3. Let $F:\mathcal J\to\mathcal C$ be an enriched functor. For a weight $W:\mathcal J\to\mathcal V$ , the $W$ –weighted limit of $F$ , if it exists, is an object $\{W,F\}\in\mathcal C$ equipped with isomorphisms

$\mathrm{Hom}_{\mathcal C}^{\mathcal V}(X,\{W,F\}) \cong \mathrm{Nat}(W,\mathrm{Hom}_{\mathcal C}^{\mathcal V}(X,F))$

natural in $X$ . Dually, given a weight $W:\mathcal J^{\mathrm{op}}\to\mathcal V$ , the $W$ –weighted colimit of $F$ , if it exists, is an object $W\star F$ equipped with isomorphisms

$\mathrm{Hom}_{\mathcal C}^{\mathcal V}(W\star F,Y) \cong \mathrm{Nat}(W,\mathrm{Hom}_{\mathcal C}^{\mathcal V}(F,Y))$

Let’s cover some basic examples (see [Ke82, Ch. 3]:

Of course, if $F:\mathcal J^{(\mathcal V)}\to\mathcal C$ , then we recover conical limits as $\{\mathrm{const}_{\mathbb I},F\}$ and conical colimits as $\mathrm{const}_{\mathbb I}\star F$ .
An object can be equivalently given as a functor (picking out the object and the identity morphism), and this identification is functorial and fully faithful. Similarly, an object corresponds to a functor . The -weighted limit of satisfies the universal property that , showing that is the power of by .
- Entirely dually, if we identify some $X\in\mathcal C$ with the functor $X:\mathbf B\mathbb I\to\mathcal C$ , and identify $V\in\mathcal V$ with the functor $\mathbf B\mathbb I^{\mathrm{op}}\to\mathcal V$ , the $V$ -weighted colimit of $X$ satisfies the universal property that $\mathrm{Hom}(V\star X,Y) \cong [V,\mathrm{Hom}(X,Y)]$ , showing that $V\star X = V\odot X$ is the copower mentioned earlier.
Specialising the above example to when $\mathcal C=\mathcal V$ , we get that the internal hom is a weighted limit $[U,V] = U\pitchfork V = \{U, V\}$ , and dually the tensor product is a weighted colimit $U\otimes V=U\odot V=U\star V$ . This might explain the notation for weighted co/limits.
In fact, weighted co/limits really do seem like analogues of the monoidal structure of . In particular, if and , then for any , we have (and this isomorphism is natural), assuming all weighted co/limits involved exist.
- Analogously, if $W:\mathcal J^{\mathrm{op}}\to\mathcal V$ and $F:\mathcal J\otimes(\mathcal J')^{\mathrm{op}}\to\mathcal V$ , then for any $G:\mathcal J'\to\mathcal C$ , we have $(W\star F)\star G \cong W\star (F\star G)$ naturally (again assuming all weighted colimits involved exist).

Don’t be nervous, go out and enrich your life!

(These title puns are getting horribly out of hand…)

If we want to generalise Lemma 2 to apply to categories enriched over cosmoi, we need to rephrase it in terms of weighted limits. It might not be clear what to do right off the bat, so let’s start by coming up with a weighted analogue of Theorem 1. By squinting at the fully faithfulness isomorphism $\mathrm{Hom}(X,Y) = \mathrm{Nat}(N_X,N_Y)$ for long enough, we realise there is an almost tautological weighted limit incarnation of this statement:

Proposition 4. Given an enriched functor $S:\mathcal S\to\mathcal C$ , the functor $N:\mathcal C\to\mathbf{PSh}(\mathcal S)$ given by $N_X := h_X\circ(S^{\mathrm{op}})$ is fully faithful if and only if $X = N_X\star S$ for every $X$ .

Proof. Just spell out the universal property: $\mathrm{Hom}(N_X\star S, Y) \cong \mathrm{Nat}(N_X,\mathrm{Hom}(S,Y)) = \mathrm{Nat}(N_X,N_Y)$ . $\blacksquare$

If we want to use this to tease out the enriched analogue of Lemma 2, we need to understand whether enriched homs are still continuous in both variables. Fortunately, this is indeed the case (though perhaps it’s not as “definitional” as in the ordinary setting). Suppose $W:\mathcal J\to\mathcal V$ is a weight for the functor $F:\mathcal J\to\mathcal C$ and $X\in\mathcal C$ , then we want to see if $\mathrm{Hom}_{\mathcal C}(X, \{W, F\})$ is itself a weighted limit. Indeed:

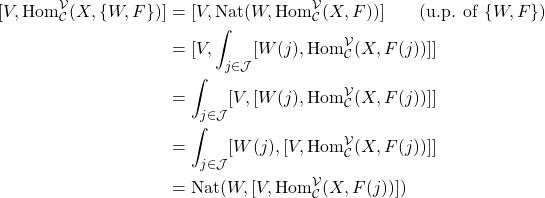
proving that $\mathrm{Hom}_{\mathcal C}(X,\{W,F\}) = \{W, \mathrm{Hom}_{\mathcal C}(X,F)\}$ . Therefore, enriched homs preserve $W$ -weighted limits in the second variable. By an entirely analogous computation, we can also show for $F:\mathcal J\to\mathcal C$ with weight $W:\mathcal J^{\mathrm{op}}\to\mathcal V$ that

$\mathrm{Hom}_{\mathcal C}(W\star F,Y) = \{W,\mathrm{Hom}_{\mathcal C}(F, Y)\}$

In particular, let’s trace this continuity of enriched homs through the statement of Proposition 4 for a dense functor $S:\mathcal S\to\mathcal V$ :

and so, just as with Lemma 2, we can see how to generalise this:

Lemma 5. For an arbitrary enriched functor $S:\mathcal S\to\mathcal C$ , we have that $\mathrm{Nat}(N_X,A) \cong \{N_X,A\}$ naturally in objects $X\in\mathcal C$ and presheaves $A:\mathcal S^{\mathrm{op}}\to\mathcal V$ .

Proof. In fact, $\mathrm{Nat}(A, B) = \{A, B\}$ for all presheaves $A, B :\mathcal S^{\mathrm{op}}\to\mathcal V$ . Indeed, this just follows from the computation

$\displaystyle [V,\mathrm{Nat}(A,B)] = [V,\int_{s\in\mathcal S}[A(s),B(s)]] = \int_{s\in\mathcal S}[V,[A(s),B(s)]] = \int_{s\in\mathcal S}[A(s),[V,B(s)]] = \mathrm{Nat}(A,[V,B])$

This seemingly simple identity can be thought of as a direct generalisation of how (conical) limits of presheaves of sets are easily computed as $\varprojlim G = \mathrm{Nat}(\mathrm{const}_{\mathrm{pt}},G)$ . $\blacksquare$

Now, if we take $\mathcal S=\mathcal C$ and $S=\mathrm{id}$ , then Lemma 5 tells us that $\mathrm{Nat}(h_X,A) \cong \{h_X,A\}$ … so we don’t exactly get a generalisation of the enriched Yoneda Lemma in this language (though it is then true that $\{h_X,A\} = A(X)$ ), but this is perhaps for the best: I have no idea how many times I implicitly rely on the uniqueness of weighted co/limits, and this formally requires the enriched Yoneda Lemma to be true.

On the other hand, as we can see from the proof, Lemma 5 is just a special case of a general universal property of the natural transformations between presheaves… so is Lemma 2 also just a special case of a general fact of natural transformations of ordinary presheaves?

C’mon, I wouldn’t ask if I didn’t know! ^{_{(Yes I would…)}} To save you the trouble of scrolling up, Lemma 2 states that

$\displaystyle\mathrm{Nat}(N_X,A) = \varprojlim((S\downarrow X)^{\mathrm{op}}\to\mathcal S^{\mathrm{op}}\xrightarrow A\mathbf{Set})$

where $(S\downarrow X)$ is the category of pairs $(s,S(s)\to X)$ . This is a comma category, but its objects are so intimately related to $N_X$ : I mean, for every $s\in\mathcal S$ , the morphisms $S(s)\to X$ are just the elements of $N_X(s)$ ! What I’m trying to say here is that $(S\downarrow X)$ is nothing more than the category of elements of $N_X$ !

Lemma 6. For $A,B:\mathcal C^{\mathrm{op}}\to\mathbf{Set}$ any (ordinary) presheaves, we have that

$\displaystyle \mathrm{Nat}(A,B) \cong \varprojlim\left(\int A\to\mathcal C^{\mathrm{op}}\xrightarrow B\mathbf{Set}\right)$

and this isomorphism is natural in $A,B$ .

Proof. An element of the right hand side is a choice of elements $y_{x,a}\in B(x)$ for every $a\in A(x)$ such that for any $\phi:x'\to x$ with $A_\phi(a)=a'$ , we have that $B_\phi(y_{x,a})=y_{x',a'}$ . This means every $y_x$ is a function $A(x)\to B(x)$ , and this compatibility constraint is equivalent to saying that these functions define a natural transformation $y:A\Rightarrow B$ . $\blacksquare$